Определение уравнения линии, примеры линии на плоскости. Приведение кривой второго порядка к каноническому виду условие параллельности прямых

Важнейшим понятием аналитической геометрии является уравнение линии на плоскости .

Определение. Уравнением линии (кривой) на плоскости Oxy называется уравнение, которому удовлетворяют координаты x и y каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии (рис.1).

В общем случае уравнение линии может быть записано в виде F(x,y)=0 или y=f(x).

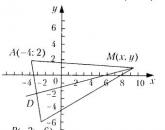
Пример. Найти уравнение множества точек, равноудаленных от точек А(-4;2), B(-2;-6).

Решение. Если M(x;y) – произвольная точка искомой линии (рис.2), то имеем AM=BM или

После преобразований получим

Очевидно, что это уравнение прямой MD – перпендикуляра, восстановленного из середины отрезка AB .

Из всех линий на плоскости особое значение имеет прямая линия . Она является графиком линейной функции, используемой в наиболее часто встречающихся на практике линейных экономико-математических моделях.

Различные виды уравнения прямой:

1)с угловым коэффициентом k и начальной ординатой b :

y = kx + b ,

где – угол между прямой и положительным направлением оси ОХ (рис. 3).

Особые случаи:

– прямая проходит через начало координат (рис.4):

– биссектриса первого и третьего, второго и четвертого координатных углов:

y=+x, y=-x;

– прямая параллельна оси ОХ и сама ось ОХ (рис. 5):

y=b, y=0;

– прямая параллельна оси OY и сама ось ОY (рис. 6):

x=a, x=0;

2) проходящей в данном направлении (с угловым коэффициентом) k через данную точку (рис. 7):

.

Если в приведенном уравнении k – произвольное число, то уравнение определяет пучок прямых , проходящих через точку , кроме прямой , параллельной оси Oy.

Пример А(3,-2) :

а) под углом к оси ОХ;

б) параллельно оси OY.

Решение .

а) , y-(-2)=-1(x-3) или y=-x+1;

б) х=3.

3) проходящей через две данные точки (рис. 8):

.

Пример . Составить уравнение прямой, проходящей через точки А(-5,4), В(3,-2).

Решение . ,

4) уравнение прямой в отрезках (рис.9):

где a, b – отрезки, отсекаемые на осях соответственно Ox и Oy.

Пример . Составить уравнение прямой, проходящей через точку А(2,-1) , если эта прямая отсекает от положительной полуоси Oy отрезок, вдвое больший, чем от положительной полуоси Ox (рис. 10).

Решение . По условию b=2a , тогда . Подставим координаты точки А(2,-1):

Откуда a=1,5.

Окончательно получим:

Или y=-2x+3.

5) общее уравнение прямой:

Ax+By+C=0,

где a и b не равны одновременно нулю.

Некоторые важные характеристики прямых :

1) расстояние d от точки до прямой:

.

2) угол между прямыми и соответственно:

и .

3) условие параллельности прямых:

или .

4) условие перпендикулярности прямых:

или .

Пример 1 . Составить уравнение двух прямых, проходящих через точку А(5,1) , одна из которых параллельна прямой 3x+2y-7=0 , а другая перпендикулярна той же прямой. Найти расстояние между параллельными прямыми.

Решение . Рисунок 11.

1) уравнение параллельной прямой Ax+By+C=0 :

из условия параллельности ;

взяв коэффициент пропорциональности, равный 1, получим А=3, В=2;

т.о. 3x+2y+C=0;

значение С найдем, подставив координаты т. А(5,1),

3*5+2*1+С=0, откуда С=-17;

уравнение параллельной прямой – 3x+2y-17=0.

2) уравнение перпендикулярной прямой из условия перпендикулярности будет иметь вид 2x-3y+C=0;

подставив координаты т. А(5,1) , получим 2*5-3*1+С=0 , откуда С=-7;

уравнение перпендикулярной прямой – 2x-3y-7=0.

3) расстояние между параллельными прямыми можно найти как расстояние от т. А(5,1) до дано прямой 3x+2y-7=0:

.

Пример 2 . Даны уравнения сторон треугольника:

3x-4y+24=0 (AB), 4x+3y+32=0 (BC), 2x-y-4=0 (AC).

Составить уравнение биссектрисы угла АВС .

Решение . Вначале найдем координаты вершины В треугольника:

,

откуда x=-8, y=0, т.е. В(-8,0) (рис. 12).

По свойству биссектрисы расстояния от каждой точки M(x,y) , биссектрисы BD до сторон АВ и ВС равны, т.е.

,

Получаем два уравнения

x+7y+8=0, 7x-y+56=0.

Из рисунка 12 угловой коэффициент искомой прямой отрицательный (угол с Ох тупой), следовательно, нам подходит первое уравнение x+7y+8=0 или y=-1/7x-8/7.

Рассмотрим функцию, заданную формулой (уравнением)

Этой функции, а следовательно, и уравнению (11) соответствует на плоскости вполне определенная линия, которая является графиком данной функции (см. рис. 20). Из определения графика функции следует, что эта линия состоит из тех и только тех точек плоскости координаты которых удовлетворяют уравнению (11).

Пусть теперь

Линия, являющаяся графиком этой функции, состоит из тех и только тех точек плоскости координаты которых удовлетворяют уравнению (12). Это значит, что если точка лежит на указанной линии, то ее координаты удовлетворяют уравнению (12). Если же точка не лежит на этой линии, то ее координаты уравнению (12) не удовлетворяют.

Уравнение (12) разрешено относительно у. Рассмотрим уравнение, содержащее х и у и не разрешенное относительно у, например уравнение

Покажем, что и этому уравнению в плоскости соответствует линия, а именно - окружность с центром в начале координат и радиусом, равным 2. Перепишем уравнение в виде

Его левая часть представляет собой квадрат расстояния точки от начала координат (см. § 2, п. 2, формула 3). Из равенства (14) следует, что квадрат этого расстояния равен 4.

Это значит, что любая точка , координаты которой удовлетворяют уравнению (14), а значит и уравнению (13), находится от начала координат на расстоянии, равном 2.

Геометрическое место таких точек есть окружность с центром в начале координат и радиусом 2. Эта окружность и будет линией, соответствующей уравнению (13). Координаты любой ее точки, очевидно, удовлетворяют уравнению (13). Если же точка не лежит на найденной нами окружности, то квадрат ее расстояния от начала координат будет либо больше, либо меньше 4, а это значит, что координаты такой точки уравнению (13) не удовлетворяют.

Пусть теперь, в общем случае, дано уравнение

в левой части которого стоит выражение, содержащее х и у.

Определение. Линией, определяемой уравнением (15), называется геометрическое место точек плоскости координаты которых удовлетворяют этому уравнению.

Это значит, что если линия L определяется уравнением то координаты любой точки L удовлетворяют этому уравнению, а координаты всякой точки плоскости лежащей вне L, уравнению (15) не удовлетворяют.

Уравнение (15) называется уравнением линии

Замечание. Не следует думать, что любое уравнение определяет какую-нибудь линию. Например, уравнение не определяет никакой линии. В самом деле, при любых действительных значениях и у левая часть данного уравнения положительна, а правая равна нулю, и следовательно, этому уравнению не могут удовлетворять координаты никакой точки плоскости

Линия может определяться на плоскости не только уравнением, содержащим декартовы координаты, но и уравнением в полярных координатах. Линией, определяемой уравнением в полярных координатах, называется геометрическое место точек плоскости, полярные координаты которых удовлетворяют этому уравнению.

Пример 1. Построить спираль Архимеда при .

Решение. Составим таблицу для некоторых значений полярного угла и соответствующих им значений полярного радиуса .

Строим в полярной системе координат точку , которая, очевидно, совпадает с полюсом; затем, проведя ось под углом к полярной оси, строим на этой оси точку с положительной координатой после этого аналогично строим точки с положительными значениями полярного угла и полярного радиуса (оси для этих точек на рис. 30 не указаны).

Соединив между собой точки получим одну ветвь кривой, обозначенную на рис. 30 жирной линией. При изменении от 0 до эта ветвь кривой состоит из бесконечного числа витков.

Равенство вида F(x, у) = 0 называется уравнением с двумя переменными х, у, если оно справедливо не для всяких пар чисел х, у. Говорят, что два числа х = x 0 , у = y 0 удовлетворяют некоторому уравнению вида F(x, y) = 0, если при подстановке этих чисел вместо переменных х и у в уравнение его левая часть обращается в нуль.

Уравнением данной линии (в назначенной системе координат) называется такое уравнение с двумя переменными, которому удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты каждой точки, не лежащей на ней.

В дальнейшем вместо выражения «дано уравнение линии F(x, у) = 0» мы часто будем говорить короче: дана линия F(x, у) = 0.

Если даны уравнения двух линий F(x, у)= 0 и Ф(x, у) = 0, то совместное решение системы

F(x,y) = 0, Ф(х, у) = 0

дает все точки их пересечения. Точнее, каждая пара чисел, являющаяся совместным решением этой системы, определяет одну из точек пересечения,

157. Даны точки *) M 1 (2; -2), М 2 (2; 2), M 3 (2; - 1), M 4 (3; -3), M 5 (5; -5), М 6 (3; -2). Установить, какие из данных точек лежат на линии, определенной уравнением х + y = 0, и какие не лежат на ней. Какая линия определена данным уравнением? (Изобразить ее на чертеже.)

158. На линии, определенной уравнением х 2 + у 2 = 25, найти точки, абсциссы которых равны следующим числам: 1) 0, 2) -3, 3) 5, 4) 7; на этой же линии найти точки, ординаты которых равны следующим числам: 5) 3, 6) -5, 7) -8. Какая линия определена данным уравнением? (Изобразить ее на чертеже.)

159. Установить, какие линии определяются следующими уравнениями (построить их на чертеже): 1)x - у = 0; 2) х + у = 0; 3) x - 2 = 0; 4)x + 3 = 0; 5) y - 5 = 0; 6) у + 2 = 0; 7) х = 0; 8) у = 0; 9) х 2 - хy = 0; 10) ху + у 2 = 0; 11) х 2 - у 2 = 0; 12) ху = 0; 13) у 2 - 9 = 0; 14) х 2 - 8x + 15 = 0; 15) у 2 + by + 4 = 0; 16) х 2 у - 7ху + 10y = 0; 17) у - |х|; 18) х - |у|; 19) y + |x| = 0; 20) x + |у| = 0; 21) у = |х - 1|; 22) y = |x + 2|; 23) х 2 + у 2 = 16; 24) (х - 2) 2 + {у- 1) 2 = 16; 25 (x + 5) 2 + (у-1) 2 = 9; 26) (x - 1) 2 + y 2 = 4; 27) x 2 + (y + 3) 2 = 1; 28) (x - 3) 2 + y 2 = 0; 29) x 2 + 2y 2 = 0; 30) 2x 2 + 3y 2 + 5 = 0; 31) (x - 2) 2 + (y + 3) 2 + 1 = 0.

160. Даны линии: l)x + y = 0; 2)х - у = 0; 3)x 2 + у 2 - 36 = 0; 4) х 2 + у 2 - 2х + у = 0; 5) х 2 + у 2 + 4х - 6у - 1 = 0. Определить, какие из них проходят через начало координат.

161. Даны линии: 1) х 2 + у 2 = 49; 2) {х - 3) 2 + (у + 4) 2 = 25; 3) (х + 6) 2 + (y - З) 2 = 25; 4) (х + 5) 2 + (y - 4) 2 = 9; 5) х 2 + у 2 - 12x + 16у - 0; 6) х 2 + у 2 - 2x + 8y + 7 = 0; 7) х 2 + у 2 - 6х + 4у + 12 = 0. Найти точки их пересечения: а) с осью Ох; б) с осью Оу.

162. Найти точки пересечения двух линий:

1) х 2 + у 2 - 8; х - у =0;

2) х 2 + у 2 - 16х + 4у + 18 = 0; х + у = 0;

3) х 2 + у 2 - 2х + 4у - 3 = 0; х 2 + у 2 = 25;

4) х 2 + у 2 - 8y + 10у + 40 = 0; х 2 + у 2 = 4.

163. В полярной системе координат даны точки M 1 (l; π/3),M 2 (2; 0).М 3 (2; π/4), М 4 (√3; π/6) и M 5 (1; 2/3π). Установить, какие из этих точек лежат на линии, определенной в полярных координатах уравнением р = 2cosΘ, и какие не лежат на ней. Какая линия определяется данным уравнением? (Изобразить ее на чертеже.)

164. На линии, определенной уравнением p = 3/cosΘ найти точки, полярные углы которых равны следующим числам: а) π/3 , б) - π/3, в) 0, г) π/6. Какая линия определена данным уравнением? (Построить ее на чертеже.)

165. На линии, определенной уравнением p = 1/sinΘ, найти точки, полярные радиусьмкоторых равны следующим числам: а) 1 6) 2, в) √2 . Какая линия определена данным уравнением? (Построить ее на чертеже.)

166. Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже): 1) р = 5; 2) Θ = π/2; 3) Θ = - π/4; 4) р cosΘ = 2; 5) p sinΘ = 1; 6.) p = 6cosΘ; 7) р = 10 sinΘ; 8) sinΘ = 1/2; 9) sinp = 1/2.

167. Построить на черТёЖе следующие спйралй Архимеда: 1) р = 20; 2) р = 50; 3) p = Θ/π; 4) р = -Θ/π.

168. Построить на чертеже следующие гиперболиче-ские спирали: 1) p = 1/Θ; 2) p = 5/Θ; 3) р = π/Θ; 4) р= - π/Θ

169. Построить на чертеже следующие логарифми-ческие спирали: 1) р = 2 Θ ; 2) p = (1/2) Θ .

170. Определить длины отрезков, на которые рассе-кает спираль Архимеда р = 3Θ луч, выходящий из полюса и наклоненный к полярной оси под углом Θ = π/6. Сделать чертеж.

171. На спирали Архимеда р = 5/πΘ взята точка С, полярный радиус которой равен 47. Определить, на сколько частей эта спираль рассекает полярный радиус точки С. Сделать чертеж.

172. На гиперболической спирали P = 6/Θ найти точку Р, полярный радиус которой равен 12. Сделать чертеж.

173. На логарифмической спирали р = 3 Θ найти точку P, полярный радиус которой равен 81. Сделать чертеж.

§ 9. Понятие уравнения линии.

Задание линии при помощи уравнения

Равенство вида F(x, y) = 0 называется уравнением с двумя переменными x , у, если оно справедливо не для всяких пар чисел х, у. Говорят, что два числа x = x 0 , у=у 0, удовлетворяют некоторому уравнению вида F(х, у)=0, если при подстановке этих чисел вместо переменных х и у в уравнение его левая часть обращается в нуль.

Уравнением данной линии (в назначенной системе координат) называется такое уравнение с двумя переменными , которому удовлетворяют координаты каждой точки, лежащей на этой линии , и не удовлетворяют координаты каждой точки, не лежащей на ней.

В дальнейшем вместо выражения «дано уравнение линии F(х, у) = 0» мы часто будем говорить короче: дана линия F (х, у) = 0.

Если даны уравнения двух линий F (х, у) = 0 и Ф(х, y) = Q, то совме­стное решение системы

Даёт все точки их пересечения. Точнее, каждая пара чисел , являющаяся сов­местным решением этой системы, определяет одну из точек пересечения.

1) х 2 +у 2 = 8, х-у = 0;

2) х 2 +у 2 -16x +4у +18 = 0, х + у = 0;

3) х 2 +у 2 -2x +4у -3 = 0, х 2 + у 2 = 25;

4) х 2 +у 2 -8x +10у+40 = 0, х 2 + у 2 = 4.

163. В полярной системе координат даны точки

Установить, какие из этих точек лежат на линии, определённой уравнением в полярных координатах  = 2 cos , и какие не лежат на ней. Какая линия определяется данным уравнением? (Изобразить её на чертеже:)

164. На линии, определённой уравнением  =
, найти точки , полярные углы которых равны следующим числам: а) ,б) - , в) 0, г) . Какая линия определена данным уравнением?

(Построить её на чертеже.)

165. На линии, определённой уравнением  =
, найти точки ,полярные радиусы которых равны следующим числам: а) 1, б) 2,в)
. Какая линия определена данным уравнением? (Построить её на чертеже.)

166. Установить, какие линии определяются в полярных коор­динатах следующими уравнениями (построить их на чертеже):

1)  = 5; 2)  = ; 3)  = ; 4)  cos  = 2; 5)  sin  = 1;

6)  = 6 cos ; 7)  = 10 sin ; 8) sin  =