Основное правило треугольника. Соотношения в треугольнике
228. В этой главе мы будем главным образом понимать под обозначениями отрезков AB, AC и т. д. выражающие их числа.
Мы знаем (п. 226), что если даны геометрически два отрезка a и b, то мы можем построить средний пропорциональный между ними. Пусть теперь отрезки даны не геометрически, а числами, т. е. под a и b будем понимать числа, выражающие 2 данных отрезка. Тогда нахождение среднего пропорционального отрезка сведется к нахождению числа x из пропорции a/x = x/b, где a, b и x числа. Из этой пропорции имеем:
x 2 = ab
x = √ab
229. Пусть имеем прямоугольный треугольник ABC (чер. 224).
Опустим из вершины его прямого угла (∠B прямой) перпендикуляр BD на гипотенузу AC. Тогда из п. 225 мы знаем:
1) AC/AB = AB/AD и 2) AC/BC = BC/DC.
Отсюда мы получаем:
AB 2 = AC · AD и BC 2 = AC · DC.
Сложив по частям полученные равенства, получим:
AB 2 + BC 2 = AC · AD + AC · DC = AC(AD + DC).
т. е. квадрат числа, выражающего гипотенузу, равен сумме квадратов чисел, выражающих катеты прямоугольного треугольника .
Сокращенно говорят: Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов .
Если мы дадим полученной формуле геометрическое толкование, то получим уже известную нам теорему Пифагора (п. 161):
квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах.
Из уравнения AB 2 + BC 2 = AC 2 иногда приходится находить катет прямоугольного треугольника, по гипотенузе и другому катету. Получим, напр.:
AB 2 = AC 2 – BC 2 и, следов.,
230. Найденное числовое соотношение между сторонами прямоугольного треугольника позволяет решать множество вычислительных задач. Решим некоторые из них:
1. Вычислить площадь равностороннего треугольника по данной его стороне .

Пусть ∆ABC (чер. 225) равносторонний и каждая его сторона выражается числом a (AB = BC = AC = a). Для вычисления площади этого треугольника надо узнать сначала его высоту BD, которую мы назовем чрез h. Мы знаем, что в равностороннем треугольнике высота BD делит основание AC пополам, т. е. AD = DC = a/2. Поэтому из прямоугольного треугольника DBC имеем:
BD 2 = BC 2 – DC 2 ,
h 2 = a 2 – a 2 /4 = 3a 2 /4 (выполняем вычитание).
Отсюда имеем:
 (выносим множитель из под корня).
(выносим множитель из под корня).
Следовательно, называя число, выражающее площадь нашего треугольника, чрез Q и зная, что площадь ∆ABC = (AC · BD)/2, находим:
![]()
Мы можем смотреть на эту формулу, как на один из способов измерения площади равностороннего треугольника: надо измерить его сторону в линейных единицах, возвести найденное число в квадрат, умножить полученное число на √3 и разделить на 4 - получим выражение площади в квадратных (соответствующих) единицах.
2. Стороны треугольника равны 10, 17 и 21 лин. един. Вычислить его площадь
.

Опустим высоту h в нашем треугольнике (чер. 226) на большую сторону - она непременно пройдет внутри треугольника, так как в треугольнике тупой угол может быть расположен только против большей стороны. Тогда большая сторона, = 21, разделится на 2 отрезка, один из которых обозначим чрез x (см. чертеж) - тогда другой = 21 – x. Получим два прямоугольных треугольника, из которых имеем:
h 2 = 10 2 – x 2 и h 2 = 17 2 – (21 – x) 2
Так как левые части этих уравнений одинаковы, то
10 2 – x 2 = 17 2 – (21 – x) 2
Выполняя действия получим:
10 2 – x 2 = 289 – 441 + 42x – x 2
Упрощая это уравнение, найдем:
Тогда из уравнения h 2 = 10 2 – x 2 , получим:
h 2 = 10 2 – 6 2 = 64
и, следовательно,
Тогда искомая площадь найдется:
Q = (21 · 8)/2 квад. един. = 84 квад. един.
3. Можно решить общую задачу:
как вычислить площадь треугольника по его сторонам?

Пусть стороны треугольника ABC выражены числами BC = a, AC = b и AB = c (чер. 227). Положим, что AC есть большая сторона; тогда высота BD пойдет внутри ∆ABC. Назовем: BD = h, DC = x и тогда AD = b – x.
Из ∆BDC имеем: h 2 = a 2 – x 2 .
Из ∆ABD имеем: h 2 = c 2 – (b – x) 2 ,
откуда a 2 – x 2 = c 2 – (b – x) 2 .
Решая это уравнение, последовательно получаем:
2bx = a 2 + b 2 – c 2 и x = (a 2 + b 2 – c 2)/2b.

(Последнее написано на том основании, что числителя 4a 2 b 2 – (a 2 + b 2 – c 2) 2 можно рассматривать, как равность квадратов, которую разлагаем на произведение суммы на разность).
Эту формулу преобразовывают, вводя периметр треугольника, который обозначим чрез 2p, т. е.
Вычитая по 2c из обеих частей равенства, получим:
a + b + c – 2c = 2p – 2c или a + b – c = 2(p – c):
Также найдем:
c + a – b = 2(p – b) и c – a + b = 2(p – a).
Тогда получим:

(p выражает полупериметр треугольника).
Этою формулою можно пользоваться для вычисления площади треугольника по трем его сторонам.
231. Упражнения .
232. В п. 229 мы нашли зависимость между сторонами прямоугольного треугольника. Можно найти подобную же зависимость для сторон (с присоединением еще одного отрезка) косоугольного треугольника.

Пусть имеем сначала ∆ABC (чер. 228) такой, чтобы ∠A был острый. Постараемся найти выражение для квадрата стороны BC, лежащей против этого острого угла (подобно тому, как в п. 229 нашли выражение для квадрата гипотенузы).
Построив BD ⊥ AC, получим из прямоугольного треугольника BDC:
BC 2 = BD 2 + DC 2
Заменим BD2, определяя его из ABD, откуда имеем:
BD 2 = AB 2 – AD 2 ,
а отрезок DC заменим чрез AC – AD (очевидно, что DC = AC – AD). Тогда получим:
BC 2 = AB 2 – AD 2 + (AC – AD) 2 = AB 2 – AD 2 + AC 2 – 2AC · AD + AD 2
Выполнив приведение подобных членов, найдем:
BC 2 = AB 2 + AC 2 – 2AC · AD.
Эта формула читается: квадрат стороны треугольника, лежащей против острого угла, равен сумме квадратов двух его других сторон, минус удвоенное произведение одной из этих сторон на ее отрезок от вершины острого угла до высоты .
233. Пусть теперь ∠A и ∆ABC (чер. 229) тупой. Найдем выражение для квадрата стороны BC, лежащей против тупого угла.

Построив высоту BD - она теперь расположится несколько иначе: на 228 где ∠A острый, точки D и C располагаются по одну сторону от A, а здесь, где ∠A тупой, точки D и C расположатся по разные стороны от A. Тогда из прямоугольного ∆BDC получим:
BC 2 = BD 2 + DC 2
Мы можем BD2 заменить, определяя его из прямоугольного ∆BDA:
BD 2 = AB 2 – AD 2 ,
а отрезок DC = AC + AD, что очевидно. Заменяя, получим:
BC 2 = AB 2 – AD 2 + (AC + AD) 2 = AB 2 – AD 2 + AC 2 + 2AC · AD + AD 2
Выполняя приведение подобных членов найдем:
BC 2 = AB 2 + AC 2 + 2AC · AD,
т. е. квадрат стороны треугольника, лежащей против тупого угла, равен сумме квадратов двух его других сторон, плюс удвоенное произведение одной из них на ее отрезок от вершины тупого угла до высоты
.
Эта формула, а равно и формула п. 232, допускают геометрическое истолкование, которое легко найти.
234. Пользуясь свойствами пп. 229, 232, 233, мы можем, если нам даны стороны треугольника в числах, узнать, есть ли у этого треугольника прямой или тупой угол.
Прямой или тупой угол в треугольнике может быть расположен лишь против большей стороны, каков же угол против нее, легко узнать: этот угол острый, прямой или тупой, смотря по тому, будет ли квадрат большей стороны меньше, равен или больше суммы квадратов двух других сторон.
Узнать, имеется ли прямой или тупой угол в следующих треугольниках, определяемых своими сторонами:
1) 15 дм., 13 дм. и 14 дм.; 2) 20, 29 и 21; 3) 11, 8 и 13; 4) 7, 11 и 15.
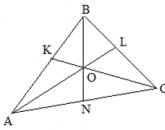
235. Пусть имеем параллелограмм ABCD (чер. 230); построим его диагонали AC и BD и его высоты BK ⊥ AD и CL ⊥ AD.

Тогда, если ∠A (∠BAD) острый, то ∠D (∠ADC) непременно тупой (ибо их сумма = 2d). Из ∆ABD, где ∠A считаем острым, имеем:
BD 2 = AB 2 + AD 2 – 2AD · AK,
а из ∆ACD, где ∠D тупой, имеем:
AC 2 = AD 2 + CD 2 + 2AD · DL.
Заменим в последней формуле отрезок AD равным ему отрезком BC и DL равным ему AK (DL = AK, ибо ∆ABK = ∆DCL, в чем легко убедиться). Тогда получим:
AC2 = BC2 + CD2 + 2AD · AK.
Сложив выражение для BD2 с последним выражением для AC 2 , найдем:
BD 2 + AC 2 = AB 2 + AD 2 + BC 2 + CD 2 ,
так как члены –2AD · AK и +2AD · AK взаимно уничтожаются. Полученное равенство можем прочитать:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
236. Вычисление медианы и биссектора треугольника по его сторонам . Пусть в треугольнике ABC (чер. 231) построена медиана BM (т. е. AM = MC). Зная стороны ∆ABC: BC = a, AC = b и AB = c, вычислить медиану BM.

Продолжим BM и отложим отрезок MD = BM. Соединив D с A и D с C, получим параллелограмм ABCD (выяснить это легко, так как ∆AMD = ∆BMC и ∆AMB = ∆DMC).
Называя медиану BM чрез m, получим BD = 2m и тогда, пользуясь предыдущим п., имеем:

237. Вычисление радиуса, описанного около треугольника круга. Пусть около ∆ABC (чер. 233) описан круг O. Построим диаметр круга BD, хорду AD и высоту треугольника BH.

Тогда ∆ABD ~ ∆BCH (∠A = ∠H = d - угол A прямой, потому что он вписанный, опирающийся на диаметр BD и ∠D = ∠C, как вписанные, опирающиеся на одну дугу AB). Поэтому имеем:
или, называя радиус OB чрез R, высоту BH чрез h и стороны AB и BC, как и раньше, соответственно чрез c и a:
но площадь ∆ABC = Q = bh/2, откуда h = 2Q/b.
Следовательно, R = (abc) / (4Q).
Мы умеем (п. 230 зад. 3) вычислять площадь треугольника Q по его сторонам. Отсюда можем вычислить R по трем сторонам треугольника.
238. Вычисление радиуса вписанного в треугольник круга. Впишем в ∆ABC, стороны которого даны (чер. 234), круг O. Соединив его центр O с вершинами треугольника и с точками касания D, E и F сторон к кругу, найдем, что радиусы круга OD, OE и OF служат высотами треугольников BOC, COA и AOB.
Называя радиус вписанного круга чрез r, имеем:

На тему «Треугольник», пожалуй, можно было бы написать целую книжку. Но книжку целиком читать слишком долго, правда? Поэтому мы здесь рассмотрим только факты, которые касаются вообще любого треугольника, а всякие специальные темы, такие как , и т.д. выделены в отдельные темы - читай книжку по кусочкам. Ну вот, что же касается любого треугольника.
1. Сумма углов треугольника. Внешний угол.
Запомни твердо и не забывай. Доказывать мы это не будем (смотри следующие уровни теории).
Единственное, что тебя может смущать в нашей формулировке - это слово «внутренних».
Зачем оно тут? А вот именно затем, чтобы подчеркнуть, что речь идёт об углах, которые внутри треугольника. А что, разве бывают ещё какие-то углы снаружи? Вот представь себе, бывают. У треугольника ещё бывают внешние углы . И самое главное следствие из того факта, что сумма внутренних углов треугольника равна, касается как раз внешнего треугольника. Так что давай выясним, что же такое этот внешний угол треугольника.
Смотри на картинку: берём треугольник и одну сторону (скажем) продолжаем.
Конечно, мы бы могли оставить сторону, а продолжить сторону. Вот так:
А вот про угол такого сказать ни в коем случае нельзя !
Так что не каждый угол снаружи треугольника имеет право называется внешним углом, а только тот, который образован одной стороной и продолжением другой стороны.
Так что же мы должны знать про внешний угол?
Смотри, на нашем рисунке это означает, что.
Как же это связано с суммой углов треугольника?
Давай разберёмся. Сумма внутренних углов равна
но - потому, что и - смежные.
Ну вот и получается: .
Видишь как просто?! Но очень важно . Так что запоминай:
Сумма внутренних углов треугольника равна, а внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
2. Неравенство треугольника
Следующий факт касается не углов, а сторон треугольника.
Это означает, что
Ты уже догадался, почему этот факт называется неравенством треугольника?
Ну вот, а где же это неравенство треугольника может оказаться полезным?
А представь, что у тебя есть три друга: Коля, Петя и Сергей. И вот, Коля говорит: «От моего дома до Петиного м по прямой». А Петя: «От моего дома до дома Сергея метров по прямой». А Сергей: «Вам хорошо, а от моего дома до Колиного аж м по прямой». Ну, тут уже ты должен сказать: «Стоп, стоп! Кто - то из вас говорит неправду!»
Почему? Да потому что если от Коли до Пети м, а от Пети до Сергея м, то от Коли до Сергея точно должно быть меньше () метров - иначе и нарушается то самое неравенство треугольника. Ну и здравый смысл точно, естественно, нарушается: ведь всякому с детства неизвестно, что путь до прямой () должен быть короче, чем путь с заходом в точку. (). Так что неравенство треугольника просто отражает этот общеизвестный факт. Ну вот, ты теперь знаешь, как отвечать на такой, скажем, вопрос:
Бывает ли треугольник со сторонами?
Ты должен проверить, правда ли, что любые два числа из этих трёх в сумме больше третьего. Проверяем: , значит, треугольника со сторонами и не бывает! А вот со сторонами - бывает, потому что
3. Равенство треугольников
Ну вот, а если не один, а два или больше треугольников. Как проверишь, равны ли они? Вообще-то по определению:
Но…это ужасно неудобное определение! Как, скажите на милость, накладывать два треугольника хотя бы даже в тетради?! Но на наше счастье есть признаки равенства треугольников , которые позволяют действовать умом, не подвергая риску тетрадки.
Да и к тому же, отбросив легкомысленные шуточки, открою тебе секрет: для математика слово «наложить треугольники» означает вовсе не вырезать их и наложить, а сказать много - много - много слов, которые будет доказывать, что два треугольника совпадут при наложении. Так что ни в коем случае нельзя в работе писать «я проверил - треугольники совпадают при наложении» - тебе это не засчитают, и будут правы, потому что никто не гарантирует, что ты при наложении не ошибся, скажем, на четверть миллиметра.
Итак, какие-то математики сказали кучу слов, мы за ними эти слова повторять не будем (разве что в последнем уровне теории), а будем активно пользоваться тремя признаками равенства треугольников.



В обиходе (математическом) приняты такие укороченные формулировки - их легче запомнить и применять.
- Первый признак - по двум сторонам и углу между ними;
- Второй признак - по двум углам и прилежащей стороне;
- Третий признак - по трём сторонам.
ТРЕУГОЛЬНИК. КОРОТКО О ГЛАВНОМ
Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Основные понятия.
Основные свойства:
- Сумма внутренних углов любого треугольника равна, т.е.
- Внешний угол треугольника равен сумме двух внутренних, не смежных с ним, т.е.
или - Сумма длин любых двух сторон треугольника больше длины его третьей стороны, т.е.
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол, т.е.
если, то, и наоборот,
если, то.
Признаки равенства треугольников.
1. Первый признак
- по двум сторонам и углу между ними.
2. Второй признак
- по двум углам и прилежащей стороне.
3. Третий признак
- по трём сторонам.
Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ЕГЭ, для поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это - не главное.
Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю...
Но, думай сам...
Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?
НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время .
И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.
Это как в спорте - нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можно воспользоваться нашими задачами (не обязательно) и мы их, конечно, рекомендуем.
Для того, чтобы набить руку с помощью наших задач нужно помочь продлить жизнь учебнику YouClever, который ты сейчас читаешь.
Как? Есть два варианта:
- Открой доступ ко всем скрытым задачам в этой статье -
- Открой доступ ко всем скрытым задачам во всех 99-ти статьях учебника - Купить учебник - 499 руб
Да, у нас в учебнике 99 таких статей и доступ для всех задач и всех скрытых текстов в них можно открыть сразу.
Доступ ко всем скрытым задачам предоставляется на ВСЕ время существования сайта.
И в заключение...
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” - это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Стандартные обозначения
Треугольник с вершинами A , B и C обозначается как (см. рис.). Треугольник имеет три стороны:
Длины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):
Треугольник имеет следующие углы:
Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α, β, γ).
Признаки равенства треугольников
Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:
- a, b, γ (равенство по двум сторонам и углу лежащему между ними);
- a, β, γ (равенство по стороне и двум прилежащим углам);
- a, b, c (равенство по трём сторонам).
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.
Некоторые точки в треугольнике - «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли . Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это - точки Аполлония . Точки и такие, что и называются точками Брокара .
Прямые
В любом треугольнике центр тяжести, ортоцентр и центр описанной окружности лежат на одной прямой, называемой прямой Эйлера .
Прямая, проходящая через центр описанной окружности и точку Лемуана, называется осью Брокара . На ней лежат точки Аполлония. Также на одной прямой лежат точки Торричелли и точка Лемуана. Основания внешних биссектрис углов треугольника лежат на одной прямой, называемой осью внешних биссектрис . На одной прямой лежат также точки пересечения прямых, содержащих стороны ортотреугольника, с прямыми, содержащими стороны треугольника. Эта прямая называется ортоцентрической осью , она перпендикулярна прямой Эйлера.
Если на описанной окружности треугольника взять точку, то её проекции на стороны треугольника будут лежать на одной прямой, называемой прямой Симсона данной точки. Прямые Симсона диаметрально противоположных точек перпендикулярны.
Треугольники
- Треугольник с вершинами в основаниях чевиан, проведённых через данную точку, называется чевианным треугольником этой точки.
- Треугольник с вершинами в проекциях данной точки на стороны называется подерным или педальным треугольником этой точки.
- Треугольник в вершинами во вторых точках пересечения прямых, проведённых через вершины и данную точку, с описанной окружностью, называют окружностно-чевианным треугольником . Окружностно-чевианный треугольник подобен подерному.
Окружности
- Вписанная окружность - окружность , касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром .
- Описанная окружность - окружность, проходящая через все три вершины треугольника. Описанная окружность также единственна.
- Вневписанная окружность - окружность, касающаяся одной стороны треугольника и продолжения двух других сторон. Таких окружностей в треугольнике три. Их радикальный центр - центр вписанной окружности срединного треугольника, называемый точкой Шпикера .
Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек или окружностью Эйлера . Центр окружности девяти точек лежит на прямой Эйлера. Окружность девяти точек касается вписанной окружности и трёх вневписанных. Точка касания вписанной окружности и окружности девяти точек называется точкой Фейербаха . Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, ортезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности - окружности Конвея . В любой треугольник можно вписать три окружности таким образом, что каждая из них касается двух сторон треугольника и двух других окружностей. Такие окружности называются окружностями Мальфатти . Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна .
В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера . Отрезки, соединяющие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера . Она служит центром гомотетии , которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.
Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна , а отрезки, соединяющие вершины с точками касания вневписанных окружностей - в точке Нагеля .
Эллипсы, параболы и гиперболы

Вписанная коника (эллипс) и её перспектор
В треугольник можно вписать бесконечно много коник (эллипсов , парабол или гипербол). Если в треугольник вписать произвольную конику и соединить точки касания с противоположными вершинами, то получившиеся прямые пересекутся в одной точке, называемой перспектором коники. Для любой точки плоскости, не лежащей на стороне или на её продолжении существует вписанная коника с перспектором в этой точке.

Описанный эллипс Штейнера и чевианы, проходящие через его фокусы
В треугольник можно вписать эллипс, который касается сторон в серединах. Такой эллипс называется вписанным эллипсом Штейнера (его перспектором будет центроид треугольника). Описанный эллипс, который касается прямых, проходящих через вершины параллельно сторонам, называется описанным эллипсом Штейнера . Если аффинным преобразованием («перекосом») перевести треугольник в правильный, то его вписанный и описанный эллипс Штейнера перейдут во вписанную и описанную окружности. Чевианы, проведённые через фокусы описанного эллипса Штейнера (точки Скутина), равны (теорема Скутина). Изо всех описанных эллипсов описанный эллипс Штейнера имеет наименьшую площадь, а изо всех вписанных наибольшую площадь имеет вписанный эллипс Штейнера.

Эллипс Брокара и его перспектор - точка Лемуана
Эллипс с фокусами в точках Брокара называется эллипсом Брокара . Его перспектором служит точка Лемуана.

Свойства вписанной параболы

Парабола Киперта
Перспекторы вписанных парабол лежат на описанном эллипсе Штейнера. Фокус вписанной параболы лежит на описанной окружности, а директриса проходит через ортоцентр. Парабола, вписанная в треугольник, имеющая директрисой прямую Эйлера, называется параболой Киперта . Её перспектор - четвёртая точка пересечения описанной окружности и описанного эллипса Штейнера, называемая точкой Штейнера .

Гипербола Киперта
Если описанная гипербола проходит через точку пересечения высот, то она равносторонняя (то есть её асимптоты перпендикулярны). Точка пересечения асимптот равносторонней гиперболы лежит на окружности девяти точек.
Преобразования
Если прямые, проходящие через вершины и некоторую точку, не лежащую на сторонах и их продолжениях, отразить относительно соответствующих биссектрис, то их образы также пересекутся в одной точке, которая называется изогонально сопряжённой исходной (если точка лежала на описанной окружности, то получившиеся прямые будут параллельны). Изогонально сопряжёнными являются многие пары замечательных точек : центр описанной окружности и ортоцентр, центроид и точка Лемуана, точки Брокара. Точки Аполлония изогонально сопряжены точкам Торричелли, а центр вписанной окружности изогонально сопряжён сам себе. Под действием изогонального сопряжения прямые переходят в описанные коники, а описанные коники - в прямые. Так, изогонально сопряжены гипербола Киперта и ось Брокара, гипербола Енжабека и прямая Эйлера, гипербола Фейербаха и линия центров вписанной о описанной окружностей. Описанные окружности подерных треугольников изогонально сопряжённых точек совпадают. Фокусы вписанных эллипсов изогонально сопряжены.
Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением . Оно также переводит прямые в описанные коники. Изотомически сопряжены точки Жергонна и Нагеля. При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в бесконечно удалённую прямую перейдёт описанный эллипс Штейнера.
Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием . Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция - проективное преобразование , которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.
Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной полярой исходной точки. Ортоцентрическая ось - трилинейная поляра ортоцентра; трилинейной полярой центра вписанной окружности служит ось внешних биссектрис. Трилинейные поляры точек, лежищих на описанной конике, пересекаются в одной точке (для описанной окружности это точка Лемуана, для описанного эллипса Штейнера - центроид). Композиция изогонального (или изотомического) сопряжения и трилинейной поляры является преобразованием двойственности (если точка, изогонально (изотомически) сопряжённая точке , лежит на трилинейной поляре точки , то трилинейная поляра точки, изогонально (изотомически) сопряжённой точке лежит на трилинейной поляре точки ).
Кубики
Соотношения в треугольнике
Примечание: в данном разделе , , - это длины трёх сторон треугольника, и , , - это углы, лежащие соответственно напротив этих трёх сторон (противолежащие углы).
Неравенство треугольника
В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном - равна. Иначе говоря, длины сторон треугольника связаны следующими неравенствами:
Неравенство треугольника является одной из аксиом метрики .
Теорема о сумме углов треугольника
Теорема синусов
,где R - радиус окружности, описанной вокруг треугольника. Из теоремы следует, что если a < b < c, то α < β < γ.
Теорема косинусов
Теорема тангенсов
Прочие соотношения
Метрические соотношения в треугольнике приведены для :
Решение треугольников
Вычисление неизвестных сторон и углов треугольника, исходя из известных, исторически получило название «решения треугольников» . При этом используются приведенные выше общие тригонометрические теоремы.
Площадь треугольника
Частные случаи ОбозначенияДля площади справедливы неравенства:
Вычисление площади треугольника в пространстве с помощью векторов
Пусть вершины треугольника находятся в точках , , .
Введём вектор площади . Длина этого вектора равна площади треугольника, а направлен он по нормали к плоскости треугольника:
Положим , где , , - проекции треугольника на координатные плоскости. При этом
и аналогично
Площадь треугольника равна .
Альтернативой служит вычисление длин сторон (по теореме Пифагора) и далее по формуле Герона .
Теоремы о треугольниках
Теорема Дезарга : если два треугольника перспективны (прямые, проходящие через соответственные вершины треугольников, пересекаются в одной точке), то их соответственные стороны пересекаются на одной прямой.
Теорема Сонда́ : если два треугольника перспективны и ортологичны (перпендикуляры, опущенные из вершин одного треугольника на стороны, противоположные соответственным вершинам треугольника, и наоборот), то оба центра ортологии (точки пересечения этих перпендикуляров) и центр перспективы лежат на одной прямой, перпендикулярной оси перспективы (прямой из теоремы Дезарга).
Два треугольника называются равными, если их можно совместить наложением. На рисунке 1 изображены равные треугольники ABC и А 1 В 1 С 1 . Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.
Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Так, например, в равных треугольниках ABC и A 1 B 1 C 1 , изображенных на рисунке 1, против соответственно равных сторон АВ и А 1 В 1 лежат равные углы С и С 1 . Равенство треугольников ABC и А 1 В 1 С 1 будем обозначать так: Δ ABC = Δ А 1 В 1 С 1 . Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).
Доказательство. Рассмотрим треугольники ABC и A 1 B 1 C 1 , у которых АВ = A 1 B 1 , АС = A 1 C 1 ∠ А = ∠ А 1 (см. рис.2). Докажем, что Δ ABC = Δ A 1 B 1 C 1 .
Так как ∠ А = ∠ А 1 , то треугольник ABC можно наложить на треугольник А 1 В 1 С 1 так, что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А 1 В 1 и A 1 C 1 . Поскольку АВ = A 1 B 1 , АС = А 1 С 1 , то сторона АВ совместится со стороной А 1 В 1 а сторона АС - со стороной А 1 C 1 ; в частности, совместятся точки В и В 1 , С и C 1 . Следовательно, совместятся стороны ВС и В 1 С 1 . Итак, треугольники ABC и А 1 В 1 С 1 полностью совместятся, значит, они равны.
Аналогично методом наложения доказывается теорема 2.
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны ().
Пример 1. В треугольниках ABC и DEF (рис. 4)
∠ А = ∠ Е, АВ = 20 см, АС = 18 см, DE = 18 см, EF = 20 см. Сравнить треугольники ABC и DEF. Какой угол в треугольнике DEF равен углу В?
Решение. Данные треугольники равны по первому признаку. Угол F треугольника DEF равен углу В треугольника ABC, так как эти углы лежат против соответственно равных сторон DE и АС.
Пример 2. Отрезки АВ и CD (рис. 5) пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС равен 6 м?
Решение.
Треугольники АОС и BOD равны (по первому признаку): ∠ АОС = ∠ BOD (вертикальные), АО = ОВ, СО = OD (по условию).
Из равенства этих треугольников следует равенство их сторон, т. е. АС = BD. Но так как по условию АС = 6 м, то и BD = 6 м.
Популярное
- Презентация по обж на тему " история создания вооруженных сил "
- Кухулин накладывает на войско гейс
- "Несолоно хлебавши": значение фразеологизма, происхождение и толкование
- Ледокол "Челюскин": история и судьба Спасение челюскинцев летчики
- Конспект ОД в подготовительной группе ДОУ с использованием ИКТ
- Казанский национальный исследовательский технологический университет
- Красноярский государственный педагогический университет Кгпу им астафьева адрес
- Сказка о местоимении читать Сказка о том что значат местоимения
- Приведение кривой второго порядка к каноническому виду условие параллельности прямых
- Где живет королева англии