Найти координаты точек числовой окружности. Урок "числовая окружность на координатной плоскости"

Если расположить единичную числовую окружность на координатной плоскости, то для ее точек можно найти координаты. Числовую окружность располагают так, чтобы ее центр совпал с точкой начала координат плоскости, т. е. точкой O (0; 0).

Обычно на единичной числовой окружности отмечают точки соответствующие от начала отсчета на окружности

• четвертям - 0 или 2π, π/2, π, (2π)/3,
• серединам четвертей - π/4, (3π)/4, (5π)/4, (7π)/4,
• третям четвертей - π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.

На координатной плоскости при указанном выше расположении на ней единичной окружности можно найти координаты, соответствующие этим точкам окружности.

Координаты концов четвертей найти очень легко. У точки 0 окружности координата x равна 1, а y равен 0. Можно обозначить так A (0) = A (1; 0).

Конец первой четверти будет располагаться на положительной полуоси ординат. Следовательно, B (π/2) = B (0; 1).

Конец второй четверти находится на отрицательной полуоси абсцисс: C (π) = C (-1; 0).

Конец третьей четверти: D ((2π)/3) = D (0; -1).

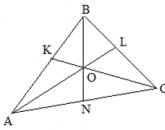
Но как найти координаты середин четвертей? Для этого строят прямоугольный треугольник. Его гипотенузой является отрезок от центра окружности (или начала координат) к точке середины четверти окружности. Это радиус окружности. Поскольку окружность единичная, то гипотенуза равна 1. Далее проводят перпендикуляр из точки окружности к любой оси. Пусть будет к оси x. Получается прямоугольный треугольник, длины катетов которого - это и есть координаты x и y точки окружности.

Четверть окружности составляет 90º. А половина четверти составляет 45º. Поскольку гипотенуза проведена к точке середины четверти, то угол между гипотенузой и катетом, выходящим из начала координат, равен 45º. Но сумма углов любого треугольника равна 180º. Следовательно, на угол между гипотенузой и другим катетом остается также 45º. Получается равнобедренный прямоугольный треугольник.

Из теоремы Пифагора получаем уравнение x 2 + y 2 = 1 2 . Поскольку x = y, а 1 2 = 1, то уравнение упрощается до x 2 + x 2 = 1. Решив его, получаем x = √½ = 1/√2 = √2/2.

Таким образом, координаты точки M 1 (π/4) = M 1 (√2/2; √2/2).

В координатах точек середин других четвертей будут меняться только знаки, а модули значений оставаться такими же, так как прямоугольный треугольник будет только переворачиваться. Получим:
M 2 ((3π)/4) = M 2 (-√2/2; √2/2)
M 3 ((5π)/4) = M 3 (-√2/2; -√2/2)
M 4 ((7π)/4) = M 4 (√2/2; -√2/2)

При определении координат третьих частей четвертей окружности также строят прямоугольный треугольник. Если брать точку π/6 и проводить перпендикуляр к оси x, то угол между гипотенузой и катетом, лежащим на оси x, составит 30º. Известно, что катет, лежащий против угла в 30º, равен половине гипотенузы. Значит, мы нашли координату y, она равна ½.

Зная длины гипотенузы и одного из катетов, по теореме Пифагора находим другой катет:
x 2 + (½) 2 = 1 2
x 2 = 1 - ¼ = ¾
x = √3/2

Таким образом T 1 (π/6) = T 1 (√3/2; ½).

Для точки второй трети первой четверти (π/3) перпендикуляр на ось лучше провести к оси y. Тогда угол при начале координат также будет 30º. Здесь уже координата x будет равна ½, а y соответственно √3/2: T 2 (π/3) = T 2 (½; √3/2).

Для других точек третей четвертей будут меняться знаки и порядок значений координат. Все точки, которые ближе расположены к оси x будут иметь по модулю значение координаты x, равное √3/2. Те точки, которые ближе к оси y, будут иметь по модулю значение y, равное √3/2.
T 3 ((2π)/3) = T 3 (-½; √3/2)
T 4 ((5π)/6) = T 4 (-√3/2; ½)
T 5 ((7π)/6) = T 5 (-√3/2; -½)
T 6 ((4π)/3) = T 6 (-½; -√3/2)
T 7 ((5π)/3) = T 7 (½; -√3/2)
T 8 ((11π)/6) = T 8 (√3/2; -½)

Числовой окружности в 10 классе уделяется достаточно много времени. Это связано со значимостью этого математического объекта для всего курса математики.

Огромное значение для хорошего усвоения материала имеет правильная подборка средств обучения. К наиболее эффективным таким средствам относятся видеоуроки. В последнее время они достигают пика популярности. Поэтому автор не стал отставать от современности и разработал в помощь учителям математики столь замечательное пособие - видеоурок по теме «Числовая окружность на координатной плоскости».

Данный урок по длительности занимает 15:22 минут. Это практически максимальное время, которое может затратить учитель на самостоятельное объяснение материала по теме. Так как на объяснение нового материала уходит столько много времени, то на закрепление необходимо подобрать самые эффективные задания и упражнения, а также выделить еще один урок, где обучающиеся будут решать задания по данной теме.

Урок начинается с изображения числовой окружности в системе координат. Автор строит эту окружность и поясняет свои действия. Затем автор называет точки пересечения числовой окружности с осями координат. Далее поясняется, какие координаты будут иметь точки окружности в разных четвертях.

После этого автор напоминает, как выглядит уравнение окружности. И вниманию слушателей представляется два макета с изображением некоторых точек на окружности. Благодаря этому, на следующем шаге автор показывает, как находятся координаты точек окружности, соответствующие определенным числам, отмеченным на шаблонах. Так получается таблица значений переменных xи y в уравнении окружности.

Далее предлагается рассмотреть пример, где необходимо определить координаты точек окружности. Перед тем, как начинать решать пример, вводится некоторое замечание, которое помогает при решении. А затем на экране появляется полное, четко структурированное и наполненное иллюстрациями решение. Здесь также присутствуют таблицы, которые облегчают понимание сущность примера.

Затем рассматриваются еще шесть примеров, которые менее трудоемкие, чем первый, но не менее важные и отражающие главную идею урока. Здесь решения представлены в полном объеме, с подробным рассказом и с элементами наглядности. А именно, в решении присутствуют рисунки, иллюстрирующие ход решения, и математическая запись, формирующая математическую грамотность обучающихся.

Учитель может ограничиться и теми примерами,которые рассмотрены в уроке, но этого может быть недостаточно для качественного усвоения материала. Поэтому подобрать задания для закрепления просто крайне важно.

Урок может быть полезен не только учителям, время которых постоянно ограничено, но и обучающимся. Особенно тем, кто получает семейное образование или занимается самообразованием. Материалами могут пользоваться те обучающиеся, которые пропустили урок по данной теме.

ТЕКСТОВАЯ РАСШИФРОВКА:

Тема нашего урока «ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ»

Мы уже знакомы с декартовой прямоугольной системой координат xOy (икс о игрек). В этой системе координат расположим числовую окружность так, чтобы центр окружности был совмещен с началом координат, а ее радиус примем за масштабный отрезок.

Начальная точка А числовой окружности совмещена с точкой с координатами (1;0) , В - с точкой (0;1), С - с (-1;0)(минус один, нуль), а D - с (0; -1)(нуль, минус один).

(смотри рис 1)

Так как каждая точка числовой окружности имеет в системе xOy (икс о игрек) свои координаты, то для точек первой четверти икх больше нуля и игрек больше нуля;

Во-второй четверти икх меньше нуля и игрек больше нуля,

для точек третьей четверти икх меньше нуля и игрек меньше нуля,

а для четвертой четверти икх больше нуля и игрек меньше нуля

Для любой точки E (x;y)(с координатами икс, игрек) числовой окружности выполняются неравенства -1≤ х≤ 1, -1≤у≤1 (икс больше либо равно минус один, но меньше либо равно один; игрек больше либо равно минус один, но меньше либо равно один).

Вспомним, что уравнение окружности радиусом R c центром в начале координат имеет вид х 2 + у 2 =R 2 (икс квадрат плюс игрек квадрат равно эр квадрат). А для единичной окружности R =1, поэтому получаем х 2 + у 2 = 1

(икс квадрат плюс игрек квадрат равно один).

Найдем координаты точек числовой окружности, которые представлены на двух макетах (см. рис 2, 3)

Пусть точка E, которая соответствует

(пи на четыре) - середина первой четверти изображенная на рисунке. Из точки E опустим перпендикуляр EK на прямую ОА и рассмотрим треугольник ОEK. Угол АОЕ =45 0 , так как дуга АЕ составляет половину дуги АВ. Следовательно, треугольник ОЕК - равнобедренный прямоугольный, у которого ОК = ЕК. Значит, абсцисса и ордината точки Е равны, т.е. икс равно игрек. Чтобы найти координаты точки Е, решим систему уравнений: (икс равно игрек- первое уравнение системы и икс квадрат плюс игрек квадрат равно один - второе уравнение системы).Во второе уравнение системы вместо х подставим у, получим 2у 2 =1(два игрек квадрат равно единице), откуда у= = (игрек равно один деленное на корень из двух равно корень из двух деленное на два) (ордината положительна).Это значит, что точка Е в прямоугольной системе координат имеет координаты(,)(корень из двух деленное на два, корень из двух деленное на два).

Рассуждая аналогично, найдем координаты для точек, соответствующих другим числам первого макета и получим: соответствует точка с координатами (- ,) (минус корень из двух деленное на два, корень из двух деленное на два); для - (- ,-) (минус корень из двух деленное на два, минус корень из двух деленное на два); для (семь пи на четыре) (,)(корень из двух деленное на два, минус корень из двух деленное на два).

Пусть точка D соответствует (рис.5). Опустим перпендикуляр из DР(дэ пэ) на ОА и рассмотрим треугольник ОDР. Гипотенуза этого треугольника OD равна радиусу единичной окружности, то есть единице, а угол DОР равен тридцати градусам, так как дуга АD = диги АВ(а дэ равно одной трети а бэ), а дуга АВ равна девяносто градусов. Следовательно, DР = (дэ пэ равно одной второй О дэ равно одной второй) Так как катет, лежащий против угла в тридцать градусов равен половине гипотенузы, то есть у = (игрек равно одной второй). Применяя теорему Пифагора, получим ОР 2 = ОD 2 - DР 2 (о пэ квадрат равно о дэ квадрат минус дэ пэ квадрат), но ОР = х (о пэ равно икс) . Значит, х 2 = ОD 2 - DР 2 =

значит, х 2 = (икс квадрат равно трем четвертым) и х = (икс равно корень из трех на два).

Икс положительное, т.к. находится в первой четверти. Получили, что точка D в прямоугольной системе координат имеет координаты (,) корень из трех деленное на два, одна вторая.

Рассуждая аналогичным образом, найдем координаты для точек, соответствующих другим числам второго макета и все полученные данные запишем в таблицы:

Рассмотрим примеры.

ПРИМЕР1. Найдите координаты точек числовой окружности: а) С 1 ();

б) С 2 (); в) С 3 (41π); г) С 4 (- 26π). (цэ один соответствующая тридцать пять пи на четыре, цэ два соответствующая минус сорока девяти пи на три, цэ три соответствующая сорок одному пи, цэ четыре соответствующая минус двадцати шести пи).

Решение. Воспользуемся утверждение, полученным ранее: если точка D числовой окружности соответствуют числу t, то она соответствует и любому числу вида t + 2πk(тэ плюс два пи ка), где ка -любое целое число, т.е. kϵZ (ка принадлежит зэт).

а) Получим = ∙ π = (8 +) ∙π = + 2π ∙ 4.(тридцать пять пи на четыре равно тридцать пять на четыре, умноженное на пи равно сумме восьми и трех четвертых, умноженной на пи равно три пи на четыре плюс произведение двух пи на четыре).Это значит, что числу тридцать пять пи на четыре соответствует та же точка числовой окружности, что и числу три пи на четыре. Используя таблицу 1, получим С 1 () = С 1 (- ;) .

б) Аналогично координаты С 2: = ∙ π = - (16 + ∙π = + 2π ∙ (- 8). Значит, числу

соответствует та же точка числовой окружности, что и числу. А числу соответствует на числовой окружности та же точка, что и числу

(показать второй макет и таблицу 2). Для точки имеем х = , у =.

в) 41π = 40π + π = π + 2π ∙ 20.Значит, числу 41π соответствует та же точка числовой окружности, что и числу π - это точка с координатами (-1 ; 0).

г) - 26π = 0 + 2π ∙ (- 13), то есть числу - 26π соответствует та же точка числовой окружности, что и числу ноль, - это точка с координатами (1;0).

ПРИМЕР 2. Найти на числовой окружности точки с ординатой у =

Решение. Прямая у = пересекает числовую окружность в двух точках. Одна точка соответствует числу, вторая точка соответствует числу,

Следовательно все точки получаем прибавляя полный оборот 2πk где k показывает сколько полных оборотов делает точка, т.е. получаем,

а любому числу все числа вида + 2πk. Часто в таких случаях говорят, что получили две серии значений: + 2πk, + 2πk.

ПРИМЕР 3. Найти на числовой окружности точки с абсциссой х = и записать, каким числам t они соответствуют.

Решение. Прямая х = пересекает числовую окружность в двух точках. Одна точка соответствует числу (смотри второй макет),

а значит и любому числу вида + 2πk. А вторая точка соответствует числу, а значит, и любому числу вида + 2πk. Эти две серии значений можно охватить одной записью: ± + 2πk(плюс минус два пи на три плюс два пи ка).

ПРИМЕР 4. Найти на числовой окружности точки с ординатой у > и записать, каким числам t они соответствуют.

Прямая у = пересекает числовую окружность в двух точках M и P. А неравенству у > соответствуют точки открытой дуги МР, это значит дуги без концов (то есть без и) , при движении по окружности против часовой стрелки, начиная с точки М, а заканчивая в точке Р. Значит, ядром аналитической записи дуги МР является неравенство < t < (тэ больше, чем пи на три, но меньше двух пи на три) , а сама аналитическая запись дуги имеет вид + 2πk < t < + 2πk(тэ больше, чем пи на три плюс два пи ка, но меньше двух пи на три плюс два пи ка).

ПРИМЕР5. Найти на числовой окружности точки с ординатой у < и записать, каким числам t они соответствуют.

Прямая у = пересекает числовую окружность в двух точках М и Р. А неравенству у < соответствуют точки открытой дуги РМ при движении по окружности против часовой стрелки, начиная с точки Р, а заканчивая в точке М. Значит, ядром аналитической записи дуги РМ является неравенство < t < (тэ больше, чем минус четыре пи на три, но меньше пи на три) , а сама аналитическая запись дуги имеет вид

2πk < t < + 2πk (тэ больше, чем минус четыре пи на три плюс два пи ка, но меньше пи на три плюс два пи ка).

ПРИМЕР 6. Найти на числовой окружности точки с абсциссой х > и записать, каким числам t они соответствуют.

Прямая х = пересекает числовую окружность в двух точках М и Р. Неравенству х > соответствуют точки открытой дуги РМ при движении по окружности против часовой стрелки с началом в точке Р, которая соответствует,и концом в точке М, которая соответствует. Значит, ядром аналитической записи дуги РМ является неравенство < t <

(тэ больше, чем минус два пи на три, но меньше двух пи на три), а сама аналитическая запись дуги имеет вид + 2πk < t < + 2πk (тэ больше, чем минус два пи на три плюс два пи ка, но меньше двух пи на три плюс два пи ка).

ПРИМЕР 7. Найти на числовой окружности точки с абсциссой х < и записать, каким числам t они соответствуют.

Прямая х = пересекает числовую окружность в двух точках М и Р. Неравенству х< соответствуют точки открытой дуги МР при движении по окружности против часовой стрелки с началом в точке М, которая соответствует, и концом в точке Р, которая соответствует. Значит, ядром аналитической записи дуги МР является неравенство < t <

(тэ больше, чем два пи на три, но меньше четырех пи на три), а сама аналитическая запись дуги имеет вид + 2πk < t < + 2πk (тэ больше, чем два пи на три плюс два пи ка, но меньше четырех пи на три плюс два пи ка).

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b) , а координаты любой точки окружности (х; у) , то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у , определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение .
Обратимся к формуле уравнения окружности:
R 2 = (x-a ) 2 + (y-b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x - 2 ) 2 + (y - (-3 )) 2 = 4 2
или
(x - 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x - 2) 2 + (y + 3) 2 = 16 .

Решение .
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение (x - 2) 2 + (y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
(x - 2) 2 + (y + 3) 2 = 16
(2 - 2) 2 + (3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

На этом уроке мы повторим важное свойство числовой окружности и поместим единичную числовую окружность в координатную плоскость по определенным правилам. Вспомним уравнение единичной числовой окружности и с его помощью решим несколько задач на нахождение координат точки на единичной числовой окружности. В конце урока составим таблицу координат для точек кратных π/6 и π/4.

Тема урока, повторение

Ранее мы изучили числовую окружность и выяснили её свойства (рис. 1).

Каждому действительному числу соответствует единственная точка на окружности.

Каждой точке на числовой окружности соответствует не только число но и все числа вида

Числовая окружность в координатной плоскости

Поместим окружность в координатную плоскость . По прежнему, каждому числу соответствует точка на окружности. Теперь этой точке на окружности соответствуют две координаты, как и любой точке координатной плоскости.

Наша задача - по данному числу найти не только точку, но и её координаты, и наоборот, по координатам найти одно или несколько соответствующих чисел.

Пример 1.Дана точка - середина дуги Точке соответствуют числа вида

Найти координаты точки (рис. 3).

Координаты можно найти двумя разными способами, рассмотрим их по очереди.

1. Точка лежит на окружности, R=1, значит, она удовлетворяет уравнению окружности

По условию. Мы помним, что величина центрального угла численно равна длине дуги в радианах, значит, угол Это значит также, что прямая делит первую четверть ровно пополам, значит, это прямая

Точка лежит на прямой поэтому удовлетворяет уравнению этой прямой.

Составим систему из двух уравнений.

Решив систему, получим искомые координаты.

2. Рассмотрим прямоугольный (рис. 4).

Итак, мы задали число нашли точку и её координаты. Определим также координаты симметричных ей точек (рис. 5).

Нахождение прямоугольных координат точек, криволинейные координаты которых кратны

Следующая задача - таким же образом определить координаты точек, кратных

Окружность радиуса R=1 помещена в координатную плоскость, Найти точку на окружности и её координаты (рис. 6).

Рассмотрим - прямоугольный.

Т. е. угол

Найдем координаты симметричных точек (рис. 7).

Мы задали число нашли точку на окружности, эта точка единственная, и нашли её координаты.

Решение задач

Пример 1. Дана точка Найти её прямоугольные координаты.

Точка середина третьей четверти (рис. 8).

Вывод, заключение

Мы поместили числовую окружность в координатную плоскость, научились находить по числу точку на окружности и её координаты. Эта техника лежит в основе определения синуса и косинуса, которые будут рассмотрены далее.

Список литературы

Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень)/под ред.

А. Г. Мордковича. - М.: Мнемозина, 2009. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень)/под ред.

А. Г. Мордковича. - М.: Мнемозина, 2007. Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). - М.: Просвещение, 1996. Галицкий М. Л., Мошкович М. М., Шварцбурд С. И. Углубленное изучение алгебры и математического анализа. - М.: Просвещение, 1997. Сборник задач по математике для поступающих во ВТУЗы (под ред. М. И.Сканави). - М.:Высшая школа, 1992. Мерзляк А. Г., Полонский В. Б., Якир М. С. Алгебраический тренажер. - К.: А. С.К., 1997. Саакян С. М., Гольдман А. М., Денисов Д. В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений). - М.: Просвещение, 2003. Карп А. П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики. - М.: Просвещение, 2006.

Mathematics. ru . Problems. ru . РЕШУ ЕГЭ.

Домашнее задание

Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень)/под ред. А. Г. Мордковича. - М.: Мнемозина, 2007.

Муниципальное общеобразовательное учреждение средняя общеобразовательная школа № 1

ХМАО-Югра

Разработка урока

в 10 «б» классе

по алгебре и началам анализа

Надежда Михайловна

учитель математики

г. Советский

Тема: ТРИГОНОМЕТРИЯ

Тригонометрические функции

Тригонометрические уравнения

Тригонометрические преобразования

Числовая окружность на

координатной плоскости

Преподавание предмета ведется по блочно- модульной технологии.

Данный урок один из уроков изучения нового материала. Поэтому основное время урока отводится именно на изучение нового материала, причем большую часть этой работы ученики выполняют самостоятельно.

Виды деятельности учащихся на уроке: фронтальная, самостоятельная и индивидуальная работы.

Так как на уроке необходимо проделать большую по объему работу и обязательно проконтролировать результаты ученической деятельности, используется интерактивная доска на этапах актуализации знаний и изучения нового материала. Для более наглядного представления наложения числовой окружности на координатную плоскость и для рефлексии содержания учебного материала в конце учебного занятия используются и презентации Power Point.

познавательная

Учить самостоятельно добывать знания

воспитывающая

Воспитывать собранность, ответственность, усердие

развивающая

Учить анализировать, сравнивать, строить аналогии

План урока:

1) Организационный момент, тема, цель урока 2 мин.

2) Актуализация знаний 4 мин .

3) Изучение нового материала 30 мин .

4) Рефлексия 3 мин.

5) Итог урока 1 мин.

Организационный момент

Числовая окружность

координатной плоскости

рассмотреть числовую окружность на координатной плоскости; вместе найти координаты двух точек; далее самостоятельно составить таблицы значений координат других основных точек окружности;

проверить умение находить координаты точек числовой окружности.

Актуализация знаний

В курсе геометрии 9 класса изучали следующий

материал:

На единичной полуокружности (R = 1) рассмотрели точку М с координатами х и у

Выдержки из учебника геометрии

Научившись находить координаты точки единичной окружности,

с легкостью перейдём к их другим названиям: синусам и косинусам, т.е.

к основной теме- ТРИГОНОМЕТРИЯ

Первое задание дано на интерактивной доске, где учащимся необходимо расставить точки и соответствующие им числа по местам на числовой окружности, перетащив их пальцем по доске.

Задание 1

Получили результат:

Второе задание дано на интерактивной доске. Ответы закрыты «шторой», открываются по мере решения.

Задание 2

Итог выполнения задания:

Изучение нового материала

Возьмём систему координат и на неё наложим числовую окружность так, чтобы их центры совпали, а горизонтальный радиус окружности совпал с положительным направлением оси ОХ (презентация Power Point)

В результате имеем точки, которые принадлежат одновременно числовой окружности и координатной плоскости. Рассмотрим одну из таких точек, например, точку М (презентация Power Point)

М (t )

Изобразим координаты этой точки

Найдем координаты интересующих нас точек единичной окружности, которые рассмотрели ранее со знаменателями 4, 3 , 6 и числителем π.

Найти координаты точки единичной окружности, соответствующей числу, соответственно и углу

Задание 3

(презентация Power Point)

Изобразим радиус и координаты точки

По теореме Пифагора имеем х 2 + х 2 = 12

Но углы треугольника по π/4 = 45°, значит треугольник – равнобедренный и х = у

Найти координаты точки единичной окружности, соответствующей числам (углам)

Задание 4

(презентация Power Point)

Значит у = 1/2

По теореме Пифагора

Треугольники равны по гипотенузе

и острому углу, значит их катеты равны

На предыдущем уроке учащиеся получили листы с заготовками числовых окружностей и различных таблиц.

Заполнить первую таблицу.

Задание 5

(интерактивная доска)

Сначала в таблицу внести точки окружности, кратные 2 и 4

Проверка результата:

(интерактивная доска)

Заполнить самостоятельно в таблице ординаты и абсциссы данных точек с учетом знаков координат в зависимости от того в какой четверти расположена точка, используя выше полученные длины отрезков для координат точек.

Задание 6

Один из учеников называет полученные результаты, остальные сверяют со своими ответами, затем для успешной корректировки результатов (так как эти таблицы будут использоваться далее в работе при выработке навыков и углублении знаний по теме) показывается правильно заполненная таблица на интерактивной доске.

Проверка результата:

(интерактивная доска)

Заполнить вторую таблицу.

Задание 7

(интерактивная доска)

Сначала в таблицу внести точки окружности, кратные 3 и 6

Проверка результата:

(интерактивная доска)

Заполнить самостоятельно в таблице ординаты и абсциссы данных точек

Задание 8

Проверка результата:

(интерактивная доска)

(презентация Power Point)

Проведем небольшой математический диктант с последующим самоконтролем.

1) Найдите координаты точек единичной окружности:

2 вариант

1 вариант

2) Найдите абсциссы точек единичной окружности:

1) Найдите координаты точек единичной окружности

2 вариант

1 вариант

2) Найдите абсциссы точек единичной окружности

Проверь себя

3) Найдите ординаты точек единичной окружности:

Для себя Вы можете поставить отметку «5» за 4 выполненных примера,

«4» за 3 примера и отметку «3» за 2 примера

Подведение итогов урока

1) В дальнейшем для нахождения значений синуса, косинуса, тангенса и котангенса точек и углов необходимо выучить по заполненным таблицам значения координат точек, принадлежащих первой четверти т.к. далее мы научимся выражать значения координат всех остальных точек через значения точек первой четверти;

2) Готовить теоретические вопросы к зачету.

Домашнее задание:

Итог урока

Оценка ставится наиболее активно работавшим на уроке ученикам. Работа всех учащихся не оценивается, так как ошибки исправляются сразу по ходу урока. Диктант проведен для самоконтроля, для оценивания недостаточный объем.