Сумма углов треугольника. Теорема о сумме углов треугольника

(опорный конспект)

Наглядная геометрия 7 класс. Опорный конспект № 4 Сумма углов треугольника.

Великий французский ученый XVII века Блез Паскаль в детстве любил возиться с геометрическими фигурами. Он был знаком с транспортиром и умел измерять углы. Юный исследователь заметил, что у всех треугольников сумма трех углов получается одна и та же - 180°. «Как же это доказать? - подумал Паскаль. - Ведь нельзя же проверить сумму углов у всех треугольников - их бесконечное множество». Тогда он отрезал ножницами два уголка треугольника и приложил их к третьему углу. Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие. Дальнейшая судьба мальчика была уже предопределена.

В этой теме вы познакомитесь с пятью признаками равенства прямоугольных треугольников и, пожалуй, с самым популярным свойством прямоугольного треугольника с углом 30°. Оно звучит так: катет, лежащий против угла 30°, равен половине гипотенузы. Разделив равносторонний треугольник высотой, мы сразу получим доказательство этого свойства.

ТЕОРЕМА . Сумма углов треугольника равна 180°. Для доказательства проведем через вершину прямую, параллельную основанию. Темные углы равны и серые углы равны как накрест лежащие при параллельных прямых. Темный угол, серый угол и угол при вершине образуют развернутый угол, их сумма 180°. Из теоремы следует, что углы равностороннего треугольника равны по 60° и что сумма острых углов прямоугольного треугольника равна 90°.

Внешним углом треугольника называется угол, смежный с углом треугольника. Поэтому иногда углы самого треугольника называют внутренними углами.

ТЕОРЕМА о внешнем угле треугольника . Внешний угол треугольника равен сумме двух внутренних, не смежных с ним. Действительно, внешний угол и два внутренних, не смежных с ним, дополняют закрашенный угол до 180°. Из теоремы следует, что внешний угол больше любого внутреннего, не смежного с ним.

ТЕОРЕМА о соотношениях между сторонами и углами треугольника . В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона. Отсюда следует: 1) Катет меньше гипотенузы. 2) Перпендикуляр меньше наклонной.

Расстояние от точки до прямой . Так как перпендикуляр меньше любой наклонной, проведенной из той же точки, то его длина принимается за расстояние от точки до прямой.

Неравенство треугольника . Длина любой стороны треугольника меньше суммы двух других его сторон, т. е. а < b + с , b < а + с , с < а + b . Следствие . Длина ломаной больше отрезка, соединяющего ее концы.

ПРИЗНАКИ РАВЕНСТВА
ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ

По двум катетам . Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого треугольника, то такие треугольники равны.

По катету и прилежащему острому углу . Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого треугольника, то такие треугольники равны.

По катету и противолежащему острому углу . Если катет и противолежащий ему острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему ему острому углу другого треугольника, то такие треугольники равны.

По гипотенузе и острому углу . Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны.

Доказательство этих признаков сразу сводится к одному из признаков равенства треугольников.

По катету и гипотенузе . Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

Доказательство. Приложим треугольники равными катетами. Получим равнобедренный треугольник. Его высота, проведенная из вершины, будет и медианой. Тогда у треугольников равны и вторые катеты, и треугольники равны по трем сторонам.

ТЕОРЕМА о свойстве катета, лежащего против угла 30° . Катет, лежащий против угла 30°, равен половине гипотенузы. Доказывается достроением треугольника до равностороннего.

ТЕОРЕМА о свойстве точек биссектрисы угла . Любая точка биссектрисы угла равноудалена от его сторон. Если точка равноудалена от сторон угла, то она лежит на биссектрисе угла. Доказывается проведением двух перпендикуляров к сторонам угла и рассмотрением прямоугольных треугольников.

Вторая замечательная точка . Биссектрисы треугольника пересекаются в одной точке.

Расстояние между параллельными прямыми . ТЕОРЕМА . Все точки каждой из двух параллельных прямых находятся на равном расстоянии от другой прямой. Из теоремы следует определение расстояния между параллельными прямыми.

Определение . Расстоянием между двумя параллельными прямыми называется расстояние от любой точки одной из параллельных прямых до другой прямой.

Подробные доказательства теорем

Это опорный конспект № 4 по геометрии в 7 классе . Выберите дальнейшие действия:

Цели и задачи:

Образовательные:

• повторить и обобщить знания о треугольнике;
• доказать теорему о сумме углов треугольника;
• практически убедиться в правильности формулировки теоремы;
• научиться применять полученные знания при решении задач.

Развивающие:

• развивать геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, умение самостоятельно добывать знания.

Воспитательные:

• развивать личностные качества учащихся, таких как целеустремленность, настойчивость, аккуратность, умение работать в коллективе.

Оборудование: мультимедийный проектор, треугольники из цветной бумаги, УМК «Живая математика», компьютер, экран.

Подготовительный этап: учитель дает задание ученику подготовить историческую справку о теореме «Сумма углов треугольника».

Тип урока : изучение нового материала.

Ход урока

I. Организационный момент

Приветствие. Психологический настрой учащихся на работу.

II. Разминка

С геометрической фигурой “треугольник” мы познакомились на предыдущих уроках. Давайте повторим, что нам известно о треугольнике?

Учащиеся работают по группам. Им предоставлена возможность общаться друг с другом, каждому самостоятельно строить процесс познания.

Что получилось? Каждая группа высказывает свои предложения, учитель записывает их на доске. Проводится обсуждение результатов:

Рисунок 1

III. Формулируем задачу урока

Итак, о треугольнике мы знаем уже достаточно много. Но не все. У каждого из вас на парте есть треугольники и транспортиры. Как вы думаете, какую задачу мы можем сформулировать?

Ученики формулируют задачу урока - найти сумму углов треугольника.

IV. Объяснение нового материала

Практическая часть (способствует актуализации знаний и навыков самопознания).Проведите измерения углов с помощью транспортира и найдите их сумму. Результаты запишите в тетрадь (заслушать полученные ответы). Выясняем, что сумма углов у всех получилась разная (так может получиться, потому что неточно приложили транспортир, небрежно выполнили подсчет и т.д.).

Выполните перегибания по пунктирным линиям и узнайте, чему еще равна сумма углов треугольника:

а)
Рисунок 2

б)
Рисунок 3

в)
Рисунок 4

г)
Рисунок 5

д)
Рисунок 6

После выполнения практической работы ученики формулируют ответ: Сумма углов треугольника равна градусной мере развернутого угла, т. е. 180°.

Учитель: В математике практическая работа дает возможность лишь сделать какое-то утверждение, но его нужно доказать. Утверждение, справедливость которого устанавливается путем доказательства, называется теоремой. Какую теорему мы можем сформулировать и доказать?

Ученики: Сумма углов треугольника равна 180 градусов.

Историческая справка: Свойство суммы углов треугольника было установлено еще в Древнем Египте. Доказательство, изложенное в современных учебниках, содержится в комментариях Прокла к «Началам» Евклида. Прокл утверждает, что это доказательство (рис. 8) было открыто еще пифагорейцами (5 в. до н. э.). В первой книге «Начал» Евклид излагает другое доказательство теоремы о сумме углов треугольника, которое легко понять при помощи чертежа (рис. 7):

Рисунок 7

Рисунок 8

Чертежи высвечиваются на экране через проектор.

Учитель предлагает с помощью чертежей доказать теорему.

Затем доказательство проводится с применением УМК «Живая математика» . Учитель на компьютере проецирует доказательство теоремы.

Теорема о сумме углов треугольника: «Сумма углов треугольника равна 180°»

Рисунок 9

Доказательство:

а)

Рисунок 10

б)

Рисунок 11

в)

Рисунок 12

Учащиеся в тетради делает краткую запись доказательства теоремы:

Теорема: Сумма углов треугольника равна 180°.

Рисунок 13

Дано: Δ АВС

Доказать: А + В + С = 180°.

Доказательство:

Что требовалось доказать.

V. Физ. минутка.

VI. Объяснение нового материала (продолжение)

Следствие из теоремы о сумме углов треугольника выводится учащимися самостоятельно, это способствует развитию умения формулировать собственную точку зрения, высказывать и аргументировать ее:

В любом треугольнике либо все углы острые, либо два острых угла, а третий тупой или прямой .

Если в треугольнике все углы острые, то он называется остроугольным .

Если один из углов треугольника тупой, то он называется тупоугольным .

Если один из углов треугольника прямой, то он называется прямоугольным .

Теорема о сумме углов треугольника позволяет классифицировать треугольники не только по сторонам, но и по углам. (По ходу введения видов треугольников учащимися заполняется таблица)

Таблица 1

Вид треугольника	Равнобедренный	Равносторонний	Разносторонний
Прямоугольный
Тупоугольный
Остроугольный

VII. Закрепление изученного материала.

1. Решить задачи устно:

(Чертежи высвечиваются на экране через проектор)

В 8 классе на уроках геометрии в школе ученики впервые знакомятся с понятием выпуклого многоугольника. Очень скоро они узнают, что эта фигура обладает очень интересным свойством. Какой бы сложной она ни была, сумма всех внутренних и внешних углов выпуклого многоугольника принимает строго определенное значение. В данной статье репетитор по математике и физике рассказывает о том, чему равна сумма углов выпуклого многоугольника.

Сумма внутренних углов выпуклого многоугольника

Как доказать эту формулу?

Прежде чем перейти к доказательству этого утверждения, вспомним, какой многоугольник называется выпуклым. Выпуклым называется такой многоугольник, который целиком находится по одну сторону от прямой, содержащей любую его сторону. Например такой, который изображен на этом рисунке:

Если же многоугольник не удовлетворяет указанному условию, то он называется невыпуклым. Например, такой:

Сумма внутренних углов выпуклого многоугольника равна , где — количество сторон многоугольника.

Доказательство этого факта основано на хорошо известной всем школьникам теореме о сумме углов в треугольнике. Уверен, что и вам эта теорема знакома. Сумма внутренних углов треугольника равна .

Идея состоит в том, чтобы разбить выпуклый многоугольник на несколько треугольников. Сделать это можно разными способами. В зависимости от того, какой способ мы выберем, доказательства будут немного отличаться.

1. Разобьём выпуклый многоугольник на треугольники всеми возможными диагоналями, проведёнными из какой-нибудь вершины. Легко понять, что тогда наш n-угольник разобьётся на треугольника:

Причём сумма всех углов всех получившихся треугольников равна сумме углов нашего n-угольника. Ведь каждый угол в получившихся треугольниках является частичной какого-то угла в нашем выпуклом многоугольнике. То есть искомая сумма равна .

2. Можно также выбрать точку внутри выпуклого многоугольника и соединить её со всеми вершинами. Тогда наш n-угольник разобьется на треугольников:

Причём сумма углов нашего многоугольника в этом случае будет равна сумме всех углов всех этих треугольников за вычетом центрального угла, который равен . То есть искомая сумма опять же равна .

Сумма внешних углов выпуклого многоугольника

Зададимся теперь вопросом: «Чему равна сумма внешних углов выпуклого многоугольника?» Ответить на этот вопрос можно следующим образом. Каждый внешний угол является смежным с соответствующим внутренним. Поэтому он равен :

Тогда сумма всех внешних углов равна . То есть она равна .

То есть получается весьма забавный результат. Если отложить последовательно друг за другом все внешние углы любого выпуклого n-угольника, то в результате заполнится ровно вся плоскости.

Этот интересный факт можно проиллюстрировать следующим образом. Давайте пропорциональном уменьшать все стороны какого-нибудь выпуклого многоугольника до тех пор, пока он не сольётся в точку. После того, как это произойдёт, все внешние углы окажутся отложенными один от другого и заполнят таким образом всю плоскость.

Интересный факт, не правда ли? И таких фактов в геометрии очень много. Так что учите геометрию, дорогие школьники!

Материал о том, чему равна сумма углов выпуклого многоугольника, подготовил , Сергей Валерьевич

Разделы: Математика

Презентация . (Слайд 1)

Тип урока: урок изучения нового материала.

Цели урока:

• Образовательные :
  • рассмотреть теорему о сумме углов треугольника,
  • показать применение теоремы при решении задач.
• Воспитательные :
  • воспитание положительного отношения учащихся к знаниям,
  • воспитывать в учащихся средствами урока уверенность в своих силах.
• Развивающие :
  • развитие аналитического мышления,
  • развитие «умений учиться»: использовать знания, умения и навыки в учебном процессе,
  • развитие логического мышления, способности четко формулировать свои мысли.

Оборудование: интерактивная доска, презентация, карточки.

ХОД УРОКА

I. Организационный момент

– Сегодня на уроке мы вспомним определения прямоугольного, равнобедренного, равностороннего треугольников. Повторим свойства углов треугольников. Применяя свойства внутренних односторонних и внутренних накрест лежащих углов докажем теорему о сумме углов треугольника и научимся применять ее при решении задач.

II. Устно (Слайд 2)

1) Найти на рисунках прямоугольный, равнобедренный, равносторонний треугольники.
2) Дать определение этим треугольникам.
3) Сформулировать свойства углов равностороннего и равнобедренного треугольника.

4) На рисунке KE II NH. (слайд 3)

– Укажите секущие для этих прямых
– Найти внутренние односторонние углы, внутренние накрест лежащие углы, назвать их свойства

III. Объяснение нового материала

Теорема. Сумма углов треугольника равна 180 о

По формулировке теоремы, ребята строят чертеж, записывают условие, заключение. Отвечая на вопросы, самостоятельно доказывают теорему.

Дано: Доказать:

Доказательство:

1. Через вершину В треугольника проведем прямую BD II AC.
2. Указать секущие для параллельных прямых.
3. Что можно сказать об углах CBD и ACB? (сделать запись)
4. Что мы знаем об углах CAB и ABD? (сделать запись)
5. Заменим угол CBD углом ACB
6. Сделать вывод.

IV. Закончи предложение. (Слайд 4)

1. Сумма углов треугольника равна …
2. В треугольнике один из углов равен, другой, третий угол треугольника равен …
3. Сумма острых углов прямоугольного треугольника равна …
4. Углы равнобедренного прямоугольного треугольника равны …
5. Углы равностороннего треугольника равны...
6. Если угол между боковыми сторонами равнобедренного треугольника равен 1000, то углы при основании равны …

V. Немного истории. (Слайды 5-7)

Доказательство теоремы о сумме углов треугольника «Сумма внутренних углов треугольника равна двум прямым» приписывают Пифагору (580-500 г.г. до н.э.)
Древнегреческий ученый Прокл (410-485 г.г. н.э.),

Треугольник. Остроугольный, тупоугольный и прямоугольный треугольник.

Катеты и гипотенуза. Равнобедренный и равносторонний треугольник.

Сумма углов треугольника.

Внешний угол треугольника. Признаки равенства треугольников.

Замечательные линии и точки в треугольнике: высоты, медианы,

биссектрисы,срединны e перпендикуляры, ортоцентр,

центр тяжести, центр описанного круга, центр вписанного круга.

Теорема Пифагора. Соотношение сторон в произвольномтреугольнике.

Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

Если все три угла острые (рис.20 ), то это остроугольный треугольник . Если один из углов прямой ( C, рис.21), то это прямоугольный треугольник ; стороны a , b , образующие прямой угол, называются катетами ; сторона c , противоположная прямому углу, называется гипотенузой . Если один из углов тупой ( B, рис.22), то это тупоугольный треугольник.


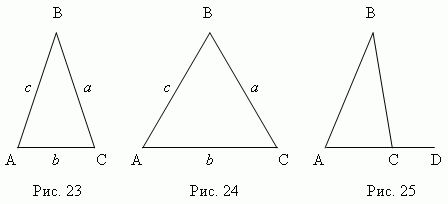
Треугольник ABC (рис.23) - равнобедренный , если две его стороны равны (a = c ); эти равные стороны называются боковыми , третья сторона называется основанием треугольника. Треугольник ABC (рис.24) – равносторонний , если все его стороны равны (a = b = c ). В общем случае (a ≠ b ≠ c ) имеем неравносторонний треугольник.

Основные свойства треугольников. В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

В частности, все углы в равностороннем треугольнике равны.

3. Сумма углов треугольника равна 180 º .

Из двух последних свойств следует, что каждый угол в равностороннем

треугольнике равен 60 º.

4. Продолжая одну из сторон треугольника (AC, рис.25), получаем внешний

угол BCD. Внешний угол треугольника равен сумме внутренних углов,

не смежных с ним : BCD = A + B.

5. Любая сторона треугольника меньше суммы двух других сторон и больше

их разности (a < b + c , a > b – c ;b < a + c , b > a – c ;c < a + b ,c > a – b ).

Признаки равенства треугольников.

Треугольники равны, если у них соответственно равны:

a ) две стороны и угол между ними;

b ) два угла и прилегающая к ним сторона;

c ) три стороны.

Признаки равенства прямоугольных треугольников.

Д ва прямоугольных треугольника равны, если выполняется одно из следующих условий:

1) равны их катеты;

2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;

4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;

5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Замечательные линии и точки в треугольнике.

Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ). Эта сторона называется основанием треугольника . Три высоты треугольника всегда пересекаются в одной точке , называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника (точка O , рис.26) расположен внутри треугольника, а ортоцентр тупоугольного треугольника (точка O , рис.27) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Медиана – это отрезок , соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника (AD , BE , CF , рис.28) пересекаются в одной точке O , всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.

Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника (AD , BE , CF , рис.29) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).

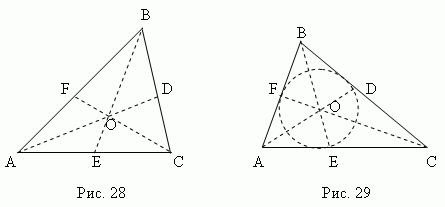
Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам ; например, на рис.29 AE : CE = AB : BC .

Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника АВС (KO , MO , NO , рис.30 ) пересекаются в одной точке О, являющейся центром описанного круга (точки K , M , N – середины сторон треугольника ABC ).

В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном - в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.

Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Доказательство теоремы Пифагора с очевидностью следует из рис.31. Рассмотрим прямоугольный треугольник ABC с катетами a , b и гипотенузой c .

Построим квадрат AKMB , используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF , сторона которого равна a + b . Теперь ясно, что площадь квадрата CDEF равна (a + b ) 2 . С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB , то есть

c 2 + 4 (ab / 2) = c 2 + 2 ab ,

отсюда ,

c 2 + 2 ab = (a + b ) 2 ,

и окончательно имеем:

c 2 = a 2 + b 2 .

Соотношение сторон в произвольном треугольнике.

В общем случае (для произвольного треугольника) имеем:

c 2 = a 2 + b 2 – 2ab · cos C,

где C – угол между сторонами a и b .